
Rotational Motion JEE Main Questions 2025 : The Rotational Motion chapter carries 3-4% of the weightage in the JEE Main Question Paper 2025. The Rotational Motion chapter includes some key topics like Moment of Inertia, Angular Momentum, and Conservation for Angular Momentum. Candidates can expect 2-4 questions from this chapter in the JEE Main 2025 exam. Students should practice the questions from the JEE Main Previous Year Question Paper to score well in the JEE Main exam. Preparing these questions and solving them will allow them to practice this chapter for the physics sections. Refer to the practice questions for the chapter here to secure good marks in JEE Main .
Check Also: JEE Main Exam Pattern
JEE Main Rotational Motion Important Questions 2025
Check the questions below and start practising them.
- A particle undergoes uniform circular motion, on which on the plane of the circle will be angular momentum of the particle remain conserved?
- Inside the circle
- Outside the circle
- On the circumference of the circle
- Centre of the circle
- A horizontal circular plate rotates at a vertical axis passing via its center with an angular velocity of Co0. A man sitting in the center has 2 blocks in his hands and tends to stretch his hands so that the moment of inertia doubles. If the K is the kinetic energy of the system, what will be the final kinetic energy?
- 2k
- K/2
- K
- K/4
- A child stands with folding hands on the center of the platform rotating about its central axis. The kinetic energy of the system is considered as K. The child will stretch out his arms to make the moment of inertia of the system double. The kinetic energy of the system will be?
- 2K
- K/2
- K/4
- 4K
- A particle is confined for rotating in a circular path along with decreasing linear speed. Then Which of the below listed options is correct
- L angular momentum is conserved about the center
- It is a spiral towards the center
- Its acceleration is toward the center
- Only the direction of L is conserved
- If “I” is the moment of inertia of a uniform square plate about an axis AB that passes via its center and is also parallel to 2 of the sides. The CD is a line of the plate that passes via the center of the plate and makes an angle of 0 with AB. The moment of inertia of the plate about the CD axis is equivalent to
- I
- I Sin 20
- I cos 20
- Icos 2(0/2)
- 2 particles each with mass-m and charge-q, are attached to the 2 ends of a light rigid rod of length ‘2R’. The rod is rotated at constant angular speed about a perpendicular axis passing via its center. The ratio of the magnitudes of the magnetic moment of the system & its angular momentum about the center of the rod is
- q/2m
- q/m
- 2q/m
- 2/πm
- The torque (T) on a body about a given point is found to be equal to AxL, in which A is the constant vector and I is the angular momentum of the body. From this, it follows that
- DI/DT is perpendicular to L at all instants of time
- The component of L in the direction of A will not change with time
- The magnitude of L will not change with time
- L will not change with time
- The solid cylinder rolls down a rough inclined plane of inclination 0 then
- The friction is dissipative
- The friction force is necessarily changing
- The friction will hinder translation but aid rotation
- The friction force will reduce if 0 is reduced
- Two point masses of 0.3kg/ 0.7kg are fixed at the endpoints of a rod which is of length 1.4m and has negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass so that the work required for rotation of the rod is minimal, check it is located at a distance of
- 0.42 m from mass of 0.3 Kg
- 0.70 m from mass of 0.7 Kg
- 0.98 m from mass of 0.3 Kg
- 0.98 m from mass of 0.7 Kg
- A mass “M” moves with a constant velocity along a line parallel to the x-axis, distant from the origin. Its angular momentum for the origin is
- Zero
- Remains constant
- Increases
- Decreases
- A cubical block of side L rests on a rough horizontal surface with a coefficient of friction P. A horizontal force F is applied on the block. If the coefficient of friction is high so that the block does not slide before toppling, the minimum force required to topple the block is:
- Mg/4
- Mg/2
- Mg (I-p)
- Infinitesimal
- A cylinder rolls up an inclined plane, reaches the height, and then again rolls down (it does not slip through these motions). The directions of the frictional force acting on the cylinder will be
- up the incline while ascending and down the incline while descending
- up the incline while ascending as well as descending
- down the incline while ascending and up the incline while descending
- down the incline while ascending as well as descending
- A smooth sphere A moves on a frictionless horizontal plane at an angular speed CO and center mass velocity. It collides elastically and head-on with B as an identical sphere. Neglect friction everywhere. After the collision, the angular speeds are 0A and 0B then?
- ധA<ധB
- ധA=ധB
- ധA=ധ
- ധB=ധ
- Consider a body in the figure below consisting of 2 identical balls each of mass M connected via a light rigirod. If an impulse J =Mv is imparted in the body at one of the ends, what would be the angular velocity?
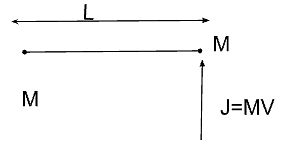
- v/L
- 2v/L
- v/3L
- v/4
- A disc with slipping rolls with angular velocity too. P and Q are two points equidistant \\um\UT\m\m\ from the center C. The order of magnitude of velocity is
- Vq>Vc>Vp
- Vp>Vc>Vq
- Vp=Vp, Vq=Vc
- Vp<Vc<Vq
- Read the passage: Two discs named A and B are mounted coaxially on a vertical axle. The discs have moments of inertia I and 21 about the common axis. Disc A is imparted an initial angular velocity of 2oa utilizing the entire potential energy of a spring compressed via a distance xr, Disc B is imparted an angular velocity to by a spring having the same spring constant and compressed by a distance x2. Both the discs rotate in a clockwise direction. Answer the following questions:.
- 2
- ½
- √2
- 1√2
- 21ധ/3t
- 91ധ/2t
- 91 ധ/4t
- 31ധ/2t

Pratice these questions to prepare for the rotational motion chapter in the physics syllabus.
Important Topics in the Rotational Motion Chapter
Candidates should familiarize themselves with the important topics in the rotational motion chapter to score well.
- Angular displacement
- Angular velocity
- Angular acceleration
- Moment of inertia
- Torque
Tips to Solve the Rotational Motion Important Questions
Here are some tips to solve the important questions in the rotational motion chapter.
- Look for more questions like this in the sample papers and the previous year's JEE Main papers.
- Solve the questions and get feedback from your mentors after solving these important questions.
- Before solving the questions, memorize all the formulas for angular displacement, angular velocity, angular acceleration, and more as given above.
- Allocate yourself a time frame to solve the questions so that you can work on your speed gradually.
Also Check:
For more articles and updates on the JEE Main 2025 Exam, stay tuned with Collegedekho !
Are you feeling lost and unsure about what career path to take after completing 12th standard?
Say goodbye to confusion and hello to a bright future!

FAQs
As per the students, the shift of 2 on April 5, 2024, was the easiest shift for the JEE Main 2024 exam.
Yes, by evaluating the trends from the past year JEE Main is a tough exam, and applicants need to make effective preparations to crack and score well in the exam.
Try not to skip any chapters, you can check the weightage of the chapters are prepare the ones with less weightage at last.
Yes, practicing the important questions for each section will help you judge your performance, you can also work on your speed by practicing these papers.
Some of the hardest topics in physics are thermodynamics & heat, mechanics, current electricity, optics, modern physics, and electromagnetic induction.
Many core concepts of rotational motion are required ot solve the JEE Main exam so we would suggest you to not skip this topic. Prepare it well to be able to score well and solve the numerical easily.
This chapter involves core concepts like angular displacement, velocity, moment of inertia, torque, and others. So it is good if you keep this chapter prepared for the JEE Main exam.
Applicants might 1-3 questions from the chapter rotational motion in the JEE Main 2025 exam. Check the weightage of the chapters before starting the preparation so that you are aware of the schedule and time needed by each chapter as per the weightage.
Was this article helpful?





















Similar Articles
GATE CS Question Paper Difficulty Level Trends: A detailed analysis
JEE Main 2026 Chemistry High Priority and Low Priority Chapters
Are JEE Main Study Groups Worth It? Detailed Pros and Cons for 2026 Aspirants
How to Prioritize Physics Chapters Based on JEE Main 2026 Weightage and Difficulty
GATE 2026 Mechanical Engineering Expected No. of Questions Topic-Wise
GATE 2026 Civil Engineering Expected No. of Questions Topic-Wise