Physics Class 12 Oscillations - Check Definitions, Important Formulas

Introduction

Oscillation refers to the process of repeated variations in any measure or quantity with respect to its equilibrium value in time. In other words, Oscillations are the periodic variations of a matter between its central value or any two values. Vibration word is usually used to describe an object’s mechanical oscillation. Although, oscillation is not only limited to mechanical systems it, also implies to dynamic systems and other fields of science. One of the most common examples of oscillation is our heart beating. Other examples include simple pendulum, tides in the sea, spring, guitar, and the list continues.

Periodic Motion

Periodic motions are movements that are repeated within equal intervals of time. For example, the earth orbiting the sun, a rocking chair, a bouncing ball, etc. have a periodic motion.

In the case of the interval of time for each cycle or repetition, we call the motion a Time Period. Meanwhile, the number of periods per unit of time is known as the Frequency. For example, the period of the Earth’s orbit is one year, and its frequency is one orbit per year.

Displacement as a Function of Time

Let us suppose there is a body that is traveling at a starting velocity of V1 at the time T1. The body further goes through acceleration ‘a’ for some time which brings it to velocity V2 at time T2. Hence, based on these assumptions, we can say:

d=Vaverage∗Δt is the displacement.

Here, assuming that the body is in constant acceleration,  Δt is the change in time.

d=(V1+V22)∗Δt

Here, V1 and V2 are starting and final velocities respectively.

Hence, the final velocity in context to starting velocity can be written as:

d=(V1+(V1 + a∗Δt)2)∗Δt

Here, a  is the constant acceleration at which the body is moving.

Rewriting the above equation, we get:

d=(2∗V12+a∗Δt2)∗Δt

This equation represents one of the most important equations of Kinematics which is also written as:

d=Vit + 12at2

Here, Vi is the initial velocity, and t is actually the change in time. All the quantities in this derivation, like Velocity, displacement, and acceleration, are vector quantities.

Hence, based on our final equation, it is evident that the change in displacement will depend on the time.

Periodic Functions and Their Application

A periodic function is a function that repeats itself within equal intervals of time. A periodic function y = f(x), having a period P, can be represented as f(X + P) = f(X). We call a function y= f(x) to be a periodic function if there exists a positive real number R such that f(x + R) = f(x), for all x belongs to real numbers. Here, the minimum value of R will be known as the fundamental period of a function, also known as the period of the function where the function repeats itself.

f(x + P) = f(x)

The sine function is a periodic function with a period of 2π. Sin(2π + x) = Sinx.

Given below are the graphs of some of the periodic functions. The graph of each of the below periodic functions has translational symmetry.

The period of a function is an important component that helps us to derive the interval at which a range of periodic functions will repeat itself. Listed below are the periods of some important periodic functions:

• The period of Sinx and Cosx is 2π.
• The period of Tanx and Cotx is π.
• The period of Secx and Cosecx is 2π.

Applications of Periodic Functions

Some of the major applications of periodic functions are listed below:

• The periodic functions graph is always symmetric and repeats itself along the horizontal axis.
• The period of a periodic function, against which the period repeats itself is equal to the constant across the entire range of the function.
• The domain of the periodic function includes all the real number values, and the range of the periodic function is defined for a fixed interval.
• If f(x) is a periodic function with a period of P, then f(ax + b) is also a periodic function with a period of P/|a|.
• If f(x) is a periodic function with a period of P, then 1/f(x) will also be a periodic function with the same fundamental period P.
• If f(x) is a periodic function with a period of P, then af(x) + b is also a periodic function with a period of P.

Also Read:

• Physics Class 12 Units and Measurements
• Physics Class 12 Motion in a Straight Line
• Physics Class 12 Laws of Motion
• Physics Class 12 Mechanical Properties of Fluid
• Physics Class 12 Mechanical Properties of Solid

Simple harmonic motion (SHM)

Simple Harmonic Motion is a special category of periodic motion. For example, the rocking chair and the sea waves from our example implement simple harmonic motion but the earth's rotation and bouncing ball don’t. But what is SHM? The simple harmonic motion definition says that it is an oscillating motion that is about an equilibrium point. We know that oscillation is a motion that gets repeated. Equilibrium is a state where the system can exist. A system that is in equilibrium is said to be at rest since all the forces on the body are perfectly balanced. A simple pendulum executes SHM as it oscillates back and forth around a point of rest, and this point occurs when the pendulum is at the lowest point in its swing and closest to the earth.

SHM Equations of Motion

The above diagram shows the maximum displacement of a sinusoid wave. It is the amplitude of the wave and can be explained by rearranging the equation for the wave position. The position of a wave exhibiting simple harmonic motion can be described using the SHM equation, i.e. x = A sin (ωt), where x is the position of the wave, A is the amplitude of the wave, ω is the wave's angular velocity, also called the angular frequency, and t is the time that the wave travels.

If we simplify this equation in terms of the SHM amplitude equation, it will be written as:

A=xsin(ωt)

Phase

Phase of a simple harmonic motion is an angular term that is used to describe the state of a body from its mean position within a specific time interval. In Simple Harmonic Motion, we represent the linear displacement of a body from its mean position in the form of sine and cosine functions.

The general SHM equation is represented by:

x=Asin(ωt+θ)

Where,

• x is the displacement of the body from its mean position at time interval ‘t’,
• A is the amplitude of S.H.M (Maximum displacement of the body from its mean position),
• ω is the angular frequency (Rate of change of phase angle per unit time),
• t is time
• θ is Initial phase at instant ‘t=0’

We call the expression:

(ωt+θ)

as the phase at instant ‘t’.

Phase difference

There there are phases of two different particles that are in Simple Harmonic Motion

(ωt+θ2)

Then the phase difference between the two particles is given by

△ϕ=(ωt+θ1)−(ωt+θ2)

Hence, with the help of the above equation, we can calculate the phase difference between two particles executing simple harmonic motion.

Oscillations of a Loaded Spring

Let us understand the Oscillations of a Loaded Spring using an example. Let us suppose that a mass m is suspended from a spring with 0 mass from a rigid support o.

Now, let us suppose that due to the load, the spring extends by a length of l to reach the state of equilibrium. Hence, the restoring force which will be set up in the spring will be given by:

Here, k is the spring constant. We see a negative sign because the restoring force is in an upward direction which is opposite to the direction of extension being in the downward direction. Since we know that the mass is in equilibrium,

Now, let us suppose that the mass is pulled further by y. So, now the restoring force will be:

In this situation, the net force on the mass will be:

Meanwhile, the produced acceleration will be:

Therefore, we can say that the acceleration is directly proportional to the displacement and is in the direction of the mean position of the object. Hence, this will be a simple harmonic motion. We can calculate the time period by the following equation:

Energy in S.H.M. Kinetic and Potential Energies

The total energy of a body when executing simple harmonic motion constitutes the energy in SHM. For example, when the pendulum is at its mean position, it is at rest and as soon as it moves towards the extreme position, it is in motion and it is again at rest when it reaches the extreme position. Therefore, in order to calculate the energy in simple harmonic motion, we need to calculate the kinetic and potential energy that the particle possesses.

Kinetic Energy (KE) in SHM

Kinetic energy refers to the energy of a body when it is in motion. If there is a body with mass m executing SHM along the path AB with O as its mean position, then OA = OB = a.

The instantaneous velocity of the particle performing S.H.M.  at a distance x from the mean position is given by

v= ±ω √a2 – x2

∴  v2 = ω2 ( a2  – x2)

∴ Kinetic energy= 1/2 mv2  = 1/2 m ω2 ( a2  – x2)

As, k/m = ω2

∴ k = m ω2

Kinetic energy= 1/2 k ( a2  – x2) .

We can use both equations Ia and Ib for calculating the kinetic energy of the particle.

Potential Energy (PE) in SHM

Potential energy refers to the energy of the body when it is at rest. If there is a particle of mass m executing SHM at distance x from its mean position, then the restoring force on the body will be F= -kx where k is the force constant.

Let us suppose that the body is further displaced at dx against the restoring force F. Let the work done to displace the particle be dw. Hence, the work done during the displacement will be:

dw = – fdx = – (- kx)dx = kxdx

Hence, the total work done to displace the particle now from 0 to x will be

∫dw=  ∫kxdx = k ∫x dx

Hence Total work done = 1/2 K x2 = 1/2 m ω2x2

The total work done here is stored in the form of potential energy.

Therefore:

Potential energy = 1/2 kx2 = 1/2 m ω2x2

These are equations of the potential energy of the particle. Thus, we can say that the potential energy is directly proportional to the square of the displacement, that is PE α x2.

Total Energy in Simple Harmonic Motion

The sum of potential energy and kinetic energy gives the total energy in SHM.

Thus, T.E. = K.E. + P.E.  = 1/2  k ( a2  – x2) + 1/2 K x2 = 1/2 k a2

Hence,

T.E.= E = 1/2 m ω2a2

The equation above is the equation of total energy in a simple harmonic motion of a particle performing the simple harmonic motion. As ω2 , a2 are constants, the total energy in the simple harmonic motion of a particle performing simple harmonic motion remains constant. Therefore, it is independent of displacement x.

As ω= 2πf , E= 1/2 m ( 2πf )2a2

∴ E=  2mπ2f 2a2

As 2 and π2 constants, we have T.E. ∼ m, T.E. ∼ f 2, and T.E. ∼ a2.

Simple Pendulum Derivation of Expression for its Time Period

Simple Pendulum is a device where the point mass is attached to a light string and is suspended from a rigid support. The mean position is the vertical line that passes through the rigid support. The vertical distance between the point of suspension and the center of mass of the suspended body (when it is in the mean position) is called the length of the simple pendulum denoted by L. This form of the pendulum is based on the resonant system having a single resonant frequency.

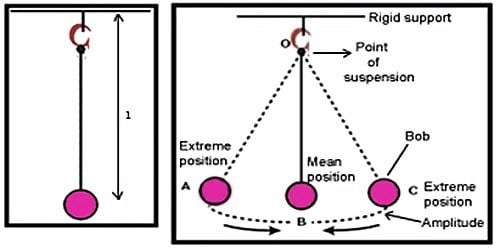
Time Period of Simple Pendulum Derivation

The equation of motion states that T – mg cosθ = mv2L

The torque T brings the mass to its equilibrium position,

τ = mgL × sinθ = mgsinθ × L = I × α

For small angles of oscillations sin θ ≈ θ,

Therefore, Iα = -mgLθ

α = -(mgLθ)/I

– ω02 θ = -(mgLθ)/I

ω02 = (mgL)/I

ω0 = √(mgL/I)

Using I = ML2, [where I is the moment of inertia of bob]

we get, ω0 = √(g/L)

Therefore, the time period of a simple pendulum is given by,

T = 2π/ω0 = 2π × √(L/g)

Oscillations: Previous Year’s Question Papers

The students can also refer to the following previous years questions to learn more about the type of questions asked in the exam:

Stay tuned to CollegeDekho for more Education News !