Physics Class 12 Waves: Types, Wave Motion, Reflection, Harmonics

Speed of Traveling Wave

A traveling wave is known as a wave that moves in space. We can graphically represent a wave too. Let’s suppose a wave is traveling along the positive direction of the X axis, then the wave can be represented by y = A sin (kx – ωt). Here, A is the amplitude, and k is the propagation constant.

Wave velocity or Phase Velocity

Wave Velocity is known as the distance covered by the wave with respect to its propagation per unit of time. Let us understand the wave velocity in terms of a wave moving in the positive X direction. If y = A sin (kx – ωt) is supposed to represent the moving wave. Let us say that this wave does not change its form while traveling through any medium. In other words, it maintains its shape. On the waveform, it retains its displacement as it moves. We must have a constant argument for a fixed point on the waveform. Hence, we have

Hence, when we differentiate both sides with respect to time t, we will get the following expressions:

We know that dx/dt = wave velocity – v, therefore

The above expression represents the wave velocity for a moving wave.

Speed of a Transverse Wave on Stretched String

There are two determining factors for the speed of transverse waves on a string including

• The tension T of the string
• The mass per unit length or the linear mass density (μ)

Speed of a Longitudinal Wave

Taking into account the dimensional analysis, the expression can determine the speed of a longitudinal wave:

Here, C is a dimensionless constant and can be shown to be unity.

Therefore, we can calculate the speed of a Longitudinal Wave using the following expressions:

Displacement Relation for a Progressive Wave

A progressive wave is a wave that consistently moves in the same direction in a medium without changing its amplitude. It is also called a traveling wave.

We can understand this using the example of a progressive wave on a string. Here, we will describe the relation of displacement of any element on the string as a function of time and the vibration of the elements of the string along the length at a given instant of time.

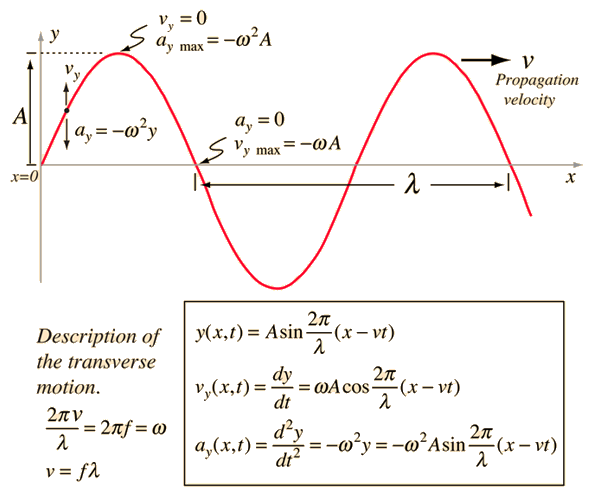
Suppose y(x,t) is the displacement of at time t and position x about the y-axis. Hence, taking into consideration the sinusoidal and periodic wave, the displacement can be represented as:

y (x, t ) = a sin (kx – ωt + φ ) (a)

The above expression can be written in the following way:

y (x, t) =A sin (kx – ωt ) + B cos (kx – ωt ), (b)

The equations (a) and (b) represent the transverse wave moving along the X-axis, where y(x,t) gives the displacement of the elements of the string at a position x at any time t. Hence, the shape of the wave can be determined at any given time.

y(x, t) = a sin (kx + ωt + φ ),

The above equation represents a transverse wave moving along the negative direction of the X-axis.

The parameters that describe a harmonic wave entirely are ‘a’, ‘φ’, ‘k’, and ‘ω’, where a is the amplitude, φ is the initial phase change, k is the angular wavenumber, and ω is the angular frequency.

The point of maximum positive displacement is called a crest, and that of maximum negative displacement is called a trough.

Amplitude

An amplitude refers to the magnitude of the maximum displacement of a particle in a wave from the equilibrium position.

Phase

The phase of the function is represented by the argument (kx – ωt + φ) of the oscillatory term sin (kx – ωt + φ). It refers to the state of motion for the waves. The point where wave travels in the same direction rise and fall together are known to be in phase with each other. The wave that travels in opposite directions, where when one rises, the other falls, is said to be in anti-phase with each other.

Wavelength

Wavelength (λ) refers to the distance between two same & identical points on a wave that is parallel to the direction of the wave. It is also known as the distance in which the shape of the wave is repeated. Wavelength can be measured in meters (m).

Angular wave number

The angular wave number represents the spatial frequency of a wave with respect to its cycles per unit distance. It is also called the number of waves that occur within a specified distance.

Angular frequency

The angular frequency refers to the angular displacement of a wave per unit of time in terms of the rate of change of phase of a waveform. It is represented by

where T is the time period of the sinusoidal function representing the wave and f is the frequency.

Principle of Superposition of Waves

The principle of superposition of waves refers to the method by which individual waveforms are added to calculate the net waveform. The principle of superposition is expressed by affirming that overlapping waves add algebraically to create a resultant wave.

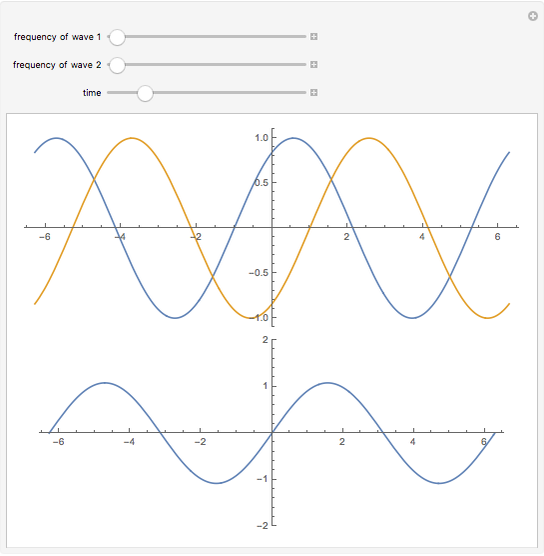
There are three different effects that can be created by the Superposition of Waves:

1. Two waves with the same frequency traveling at the same speed along the same direction in a medium will go to the state of superposition and will create the interference of waves.
2. Two waves with the same frequency traveling at the same speed along the opposite direction in a medium will go to the state of superposition and will create stationary waves.
3. Two waves with varying frequencies traveling at the same speed along the opposite direction in a medium will go to the state of superposition and will beats.

Constructive & Destructive Interference

When two waves with the same wavelength, amplitude, and frequency move in the same specific direction, they are known as Constructive & Destructive Interference. According to the superposition principle, the subsequent wave displacement can be written as:

y(x,t) = y m sin(kx-ωt) + y m sin(kx-ωt+ϕ) = 2 y m cos(ϕ/2) sin(kx-ωt+ϕ/2)

In this wave, the amplitude will depend on the phase (ϕ). So, when two waves will be in the same phase (ϕ=0), then they interfere constructively. Meanwhile, when two waves will be in opposite phases, (ϕ=180), then they interfere destructively; canceling each other out.

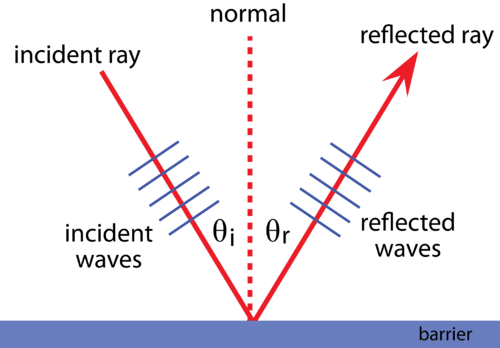
Reflection of Waves

The straight waves have troughs and crests that are alternating. Ray is the direction in which these wavefronts (straight-line crests) travel through the water and are perpendicular to the wavefront. Upon reaching the barrier placed within the water, these waves bounce off the water and head in a different direction. Regardless of the angle at which the wavefronts approach the barrier, one general law of reflection holds true: the waves will always reflect in such a way that the angle at which they approach the barrier equals the angle at which they reflect off the barrier. This is known as the law of reflection.

Standing Waves in Strings and Organ Pipes

Standing wave refers to the superposition of two waves that have the same frequency, same amplitude and are moving in opposite directions.

Suppose two waves that have the same frequency, same amplitude and are moving in opposite directions. The equation of the two waves are given by

Where, A is amplitude, k is  wave number, ω is angular frequency (ω = 2πf, f is frequency)

These waves interfere to produce what we call standing waves.

Standing Waves in Strings

Standing waves are formed on stretched strings. Nodes are formed at the rigid ends , where wedges are held under the string. Antinodes are formed in between, over the stretched string. In any mode of vibration the number of antinodes is one less than the number of nodes.

The frequency of first overtone or second harmonic is n2 = 2n1

Similarly , the frequency of the second overtone or third harmonic is n3 =3 n1 and so on.

Standing Waves in Organ Pipes

A pipe that has air with rigid walls filled in it with a diameter smaller than its length is known as an organ pipe. These pipes are used to create musical sounds when the air is pushed into the pipe. The pipe that is opened at both ends is called an open organ pipe and the pipe with only one open end is called a closed organ pipe.

• The frequency of the fundamental note or first harmonic in an open organ pipe can be presented as:

Fundamental Mode and Harmonics

The fundamental mode is known as the mode having the lowest frequency (f1). A harmonic comes under the ascending sonic components which create a sound above the audible fundamental frequency. Harmonics can be difficult to detect as single components, but they exist.

The frequencies are called overtones and harmonic series refer to the numerical pattern that connects both of them.

Harmonics often have a lower volume than fundamental modes. Harmonics are multiples of the fundamentals that are positive integers.

The relationship between harmonics and waves can be demonstrated through the table below:

Beats

Beats refer to the pulsation which is created by adding two waves that have different frequencies. The concept of beats is used in various methods such as instrument tuning. The principle is also used in the superheterodyne reception of radio waves, in which a low-frequency signal from an oscillator is beat against an incoming high-frequency radio signal to produce an intermediate (beat) frequency that can be amplified to produce audible signals.

Waves: Previous Year’s Question Papers

The students can also refer to the following previous years questions to learn more about the type of questions asked in the exam:

Stay tuned to CollegeDekho for more Education News !