JEE Main Vector Algebra Practice Questions With Solutions

Tell us your JEE Main score & access the list of colleges you may qualify for!

JEE Main Physics Vector Algebra Practice Questions

Question 1.

The angle between vector $\vec{Q}$ and the resultant of $(2 \vec{Q} + 2 \vec{P})$ and $(2 \vec{Q} - 2 \vec{P})$ is :

\tan^{- 1} (P / Q)

^{\circ}

\tan^{- 1} \frac{(2 \vec{Q} - 2 \vec{P})}{2 \vec{Q} + 2 \vec{P}}

\tan^{- 1} (2 Q / P)

Question 2.

If two vectors $\vec{A}$ and $\vec{B}$ having equal magnitude $R$ are inclined at angle $θ$ , then

| \vec{A} + \vec{B} | = 2 R \cos (\frac{θ}{2})

| \vec{A} - \vec{B} | = 2 R \cos (\frac{θ}{2})

| \vec{A} - \vec{B} | = \sqrt{2} R \sin (\frac{θ}{2})

| \vec{A} + \vec{B} | = 2 R \sin (\frac{θ}{2})

Question 3.

A vector in

x - y

plane makes an angle of

30^{\circ}

with

y

-axis. The magnitude of

y

-component of vector is

2 \sqrt{3}

. The magnitude of

x

-component of the vector will be :

\sqrt{3}

\frac{1}{\sqrt{3}}

Question 4.

When vector $\vec{A} = 2 \hat{i} + 3 \hat{j} + 2 \hat{k}$ is subtracted from vector $\vec{B}$ , it gives a vectorequal to $2 \hat{j}$ . Then the magnitude of vector $\vec{B}$ will be :

\sqrt{33}

\sqrt{6}

\sqrt{5}

Question 5.

Two forces having magnitude $A$ and $\frac{A}{2}$ are perpendicular to each other. The magnitude of their resultant is:

\frac{5 A}{2}

\frac{\sqrt{5} A}{4}

\frac{\sqrt{5} A}{2}

\frac{\sqrt{5} A^{2}}{2}

Question 6.

If two vectors $\vec{P} = \hat{i} + 2 m \hat{j} + m \hat{k}$ and $\vec{Q} = 4 \hat{i} - 2 \hat{j} + m \hat{k}$ are perpendicular to each other. Then, the value of m will be :

- 1

Question 7.

Two vectors $\vec{A}$ and $\vec{B}$ have equal magnitudes. If magnitude of $\vec{A}$ + $\vec{B}$ is equal to two times the magnitude of $\vec{A}$ $-$ $\vec{B}$ , then the angle between $\vec{A}$ and $\vec{B}$ will be :

\sin^{- 1} (\frac{3}{5})

\sin^{- 1} (\frac{1}{3})

\cos^{- 1} (\frac{3}{5})

\cos^{- 1} (\frac{1}{3})

Question 8.

$\vec{A}$ is a vector quantity such that $| \vec{A} |$ = non-zero constant. Which of the following expression is true for $\vec{A}$ ?

\vec{A} . \vec{A} = 0

\vec{A} \times \vec{A} < 0

\vec{A} \times \vec{A} = 0

\vec{A} \times \vec{A} > 0

Question 9.

Which of the following relations is true for two unit vector $\hat{A}$ and $\hat{B}$ making an angle $θ$ to each other?

| \hat{A} + \hat{B} | = | \hat{A} - \hat{B} | \tan \frac{θ}{2}

| \hat{A} - \hat{B} | = | \hat{A} + \hat{B} | \tan \frac{θ}{2}

| \hat{A} + \hat{B} | = | \hat{A} - \hat{B} | c o s \frac{θ}{2}

| \hat{A} - \hat{B} | = | \hat{A} + \hat{B} | \cos \frac{θ}{2}

Question 10.

Statement I :

Two forces

(\vec{P} + \vec{Q})

and

(\vec{P} - \vec{Q})

where

\vec{P} ⊥ \vec{Q}

, when act at an angle

θ

₁ to each other, the magnitude of their resultant is

\sqrt{3 (P^{2} + Q^{2})}

, when they act at an angle

θ

₂, the magnitude of their resultant becomes

\sqrt{2 (P^{2} + Q^{2})}

. This is possible only when

θ_{1} < θ_{2}

.

Statement II :

In the situation given above.

θ

₁ = 60

^{\circ}

and

θ

₂ = 90

^{\circ}

In the light of the above statements, choose the most appropriate answer from the options given below :-

Statement I is false but Statement II is true

Both Statement I and Statement II are true

Statement I is true but Statement II is false

Both Statement I and Statement II are false.

Question 1.

The resultant of these forces

\vec{O P}, \vec{O Q}, \vec{O R}, \vec{O S}

and

\vec{O T}

is approximately .......... N.

[Take

\sqrt{3} = 1.7

\sqrt{2} = 1.4

Given

\hat{i}

and

\hat{j}

unit vectors along x, y axis]

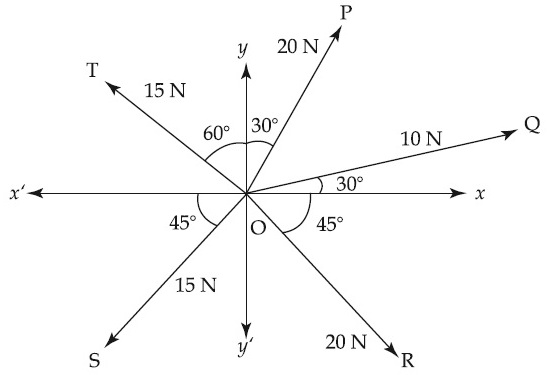
JEE Main 2021 (Online) 27th August Morning Shift Physics - Vector Algebra Question 20 English

9.25 \hat{i} + 5 \hat{j}

3 \hat{i} + 15 \hat{j}

2.5 \hat{i} - 14.5 \hat{j}

- 1.5 \hat{i} - 15.5 \hat{j}

Question 2.

The angle between vector

(\vec{A})

and

(\vec{A} - \vec{B})

is :

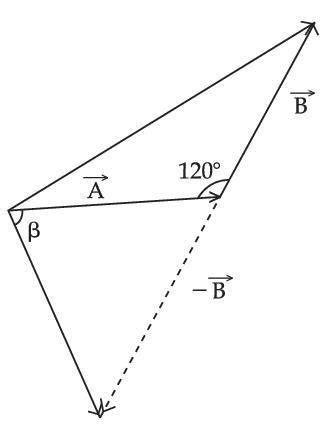
JEE Main 2021 (Online) 26th August Evening Shift Physics - Vector Algebra Question 21 English

\tan^{- 1} (\frac{- \frac{B}{2}}{A - B \frac{\sqrt{3}}{2}})

\tan^{- 1} (\frac{A}{0.7 B})

\tan^{- 1} (\frac{\sqrt{3} B}{2 A - B})

\tan^{- 1} (\frac{B \cos θ}{A - B \sin θ})

Question 3.

The magnitude of vectors

\vec{O A}

\vec{O B}

and

\vec{O C}

in the given figure are equal. The direction of

\vec{O A}

\vec{O B}

-

\vec{O C}

with x-axis will be :

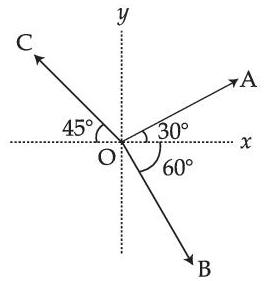
JEE Main 2021 (Online) 26th August Morning Shift Physics - Vector Algebra Question 22 English

\tan^{- 1} \frac{(1 - \sqrt{3} - \sqrt{2})}{(1 + \sqrt{3} + \sqrt{2})}

\tan^{- 1} \frac{(\sqrt{3} - 1 + \sqrt{2})}{(1 + \sqrt{3} - \sqrt{2})}

\tan^{- 1} \frac{(\sqrt{3} - 1 + \sqrt{2})}{(1 - \sqrt{3} + \sqrt{2})}

\tan^{- 1} \frac{(1 + \sqrt{3} - \sqrt{2})}{(1 - \sqrt{3} - \sqrt{2})}

Question 4.

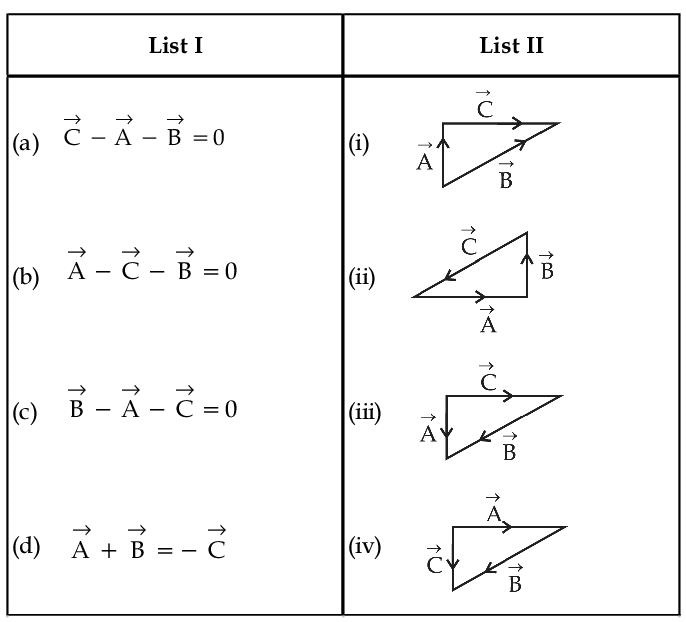
Assertion A : If A, B, C, D are four points on a semi-circular are with centre at 'O' such that

| \vec{A B} | = | \vec{B C} | = | \vec{C D} |

, then

\vec{A B} + \vec{A C} + \vec{A D} = 4 \vec{A O} + \vec{O B} + \vec{O C}

Reason R : Polygon law of vector addition yields

\vec{A B} + \vec{B C} + \vec{C D} + \vec{A D} = 2 \vec{A O}

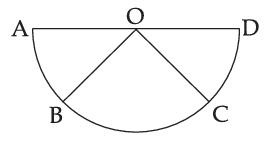
JEE Main 2021 (Online) 27th July Morning Shift Physics - Vector Algebra Question 23 English

In the light of the above statements, choose the most appropriate answer from the options given below :

A is correct but R is not correct.

A is not correct but R is correct.

Both A and R are correct and R is the correct explanation of A.

Both A and R are correct but R is not the correct explanation of A.

Question 5.

Two vectors

\vec{X}

and

\vec{Y}

have equal magnitude. The magnitude of (

\vec{X}

-

\vec{Y}

) is n times the magnitude of (

\vec{X}

\vec{Y}

). The angle between

\vec{X}

and

\vec{Y}

is :

\cos^{- 1} (\frac{- n^{2} - 1}{n^{2} - 1})

\cos^{- 1} (\frac{n^{2} - 1}{- n^{2} - 1})

\cos^{- 1} (\frac{n^{2} + 1}{- n^{2} - 1})

\cos^{- 1} (\frac{n^{2} + 1}{n^{2} - 1})

Question 6.

Match List - I with List - II

JEE Main 2021 (Online) 25th July Morning Shift Physics - Vector Algebra Question 25 English

Choose the correct answer from the options given below :

(a)

\to

(iv), (b)

\to

(i), (c)

\to

(iii), (d)

\to

(ii)

(a)

\to

(iv), (b)

\to

(iii), (c)

\to

(i), (d)

\to

(ii)

(a)

\to

(iii), (b)

\to

(ii), (c)

\to

(iv), (d)

\to

(i)

(a)

\to

(i), (b)

\to

(iv), (c)

\to

(ii), (d)

\to

(iii)

Question 7.

What will be the projection of vector

\vec{A} = \hat{i} + \hat{j} + \hat{k}

on vector

\vec{B} = \hat{i} + \hat{j}

\sqrt{2} (\hat{i} + \hat{j} + \hat{k})

(\hat{i} + \hat{j})

\sqrt{2} (\hat{i} + \hat{j})

2 (\hat{i} + \hat{j} + \hat{k})

Question 8.

Two vectors

\vec{P}

and

\vec{Q}

have equal magnitudes. If the magnitude of

\vec{P} + \vec{Q}

is n times the magnitude of

\vec{P} - \vec{Q}

, then angle between

\vec{P}

and

\vec{Q}

is :

\sin^{- 1} (\frac{n - 1}{n + 1})

\cos^{- 1} (\frac{n - 1}{n + 1})

\sin^{- 1} (\frac{n^{2} - 1}{n^{2} + 1})

\cos^{- 1} (\frac{n^{2} - 1}{n^{2} + 1})

Question 9.

\vec{A}

and

\vec{B}

are two vectors satisfying the relation

\vec{A}

\vec{B}

| \vec{A} \times \vec{B} |

. Then the value of

| \vec{A} - \vec{B} |

will be :

\sqrt{A^{2} + B^{2} + \sqrt{2} A B}

\sqrt{A^{2} + B^{2}}

\sqrt{A^{2} + B^{2} - \sqrt{2} A B}

\sqrt{A^{2} + B^{2} + 2 A B}

Question 10.

In an octagon ABCDEFGH of equal side, what is the sum of

\vec{A B} + \vec{A C} + \vec{A D} + \vec{A E} + \vec{A F} + \vec{A G} + \vec{A H}

,

if,

\vec{A O} = 2 \hat{i} + 3 \hat{j} - 4 \hat{k}

JEE Main 2021 (Online) 25th February Morning Shift Physics - Vector Algebra Question 31 English

- 16 \hat{i} - 24 \hat{j} + 32 \hat{k}

16 \hat{i} + 24 \hat{j} - 32 \hat{k}

16 \hat{i} + 24 \hat{j} + 32 \hat{k}

16 \hat{i} - 24 \hat{j} + 32 \hat{k}

Heat and Thermodynamics Practice Test Questions with Solutions Attempt Now
Gravitation Practice Test Questions with Solutions Attempt Now
Current Electricity Practice Test Questions with Solutions Attempt Now
Dual Nature of Radiation Practice Test Questions with Solutions Attempt Now
Atoms and Nuclei Practice Test Questions with Solutions Attempt Now
Units & Measurements Practice Test Questions with Solutions Attempt Now
Properties of Matter Practice Test Questions with Solutions Attempt Now
Semiconductor Practice Test Questions with Solutions Attempt Now
Electrostatics Practice Test Questions with Solutions Attempt Now
Magnetic Effect of Current Practice Test Questions with Solutions Attempt Now
Electromagnetic Waves Practice Test Questions with Solutions Attempt Now
Geometrical Optics Practice Test Questions with Solutions Attempt Now
Alternating Current Practice Test Questions with Solutions Attempt Now
Laws of Motion Practice Test Questions with Solutions Attempt Now
Simple Harmonic Motion Practice Test Questions with Solutions Attempt Now
Wave Optics Practice Test Questions with Solutions Attempt Now
Capacitor Practice Test Questions with Solutions Attempt Now
Motion in a Straight Line Practice Test Questions with Solutions Attempt Now
Rotational Motion Practice Test Questions with Solutions Attempt Now
Communication Systems Practice Test Questions with Solutions Attempt Now
Center of Mass and Collision Practice Test Questions with Solutions Attempt Now
Electromagnetic Induction Practice Test Questions with Solutions Attempt Now
Work Power & Energy Practice Test Questions with Solutions Attempt Now
Circular Motion Practice Test Questions with Solutions Attempt Now
Waves Practice Test Questions with Solutions Attempt Now
Motion in a Plane Practice Test Questions with Solutions Attempt Now
Magnetic Properties of Matter Practice Test Questions with Solutions Attempt Now

Unlock Your Results: Answer Key Available for Download

Still have questions about JEE Main ? Ask us.

Typical response between 24-48 hours
Get personalized response
Free of Cost
Access to community

JEE Main Vector Algebra Practice Questions With Solutions

JEE Main Physics Vector Algebra Practice Questions

Question 1.

Question 2.

Question 3.

Question 4.

Question 5.

Question 6.

Question 7.

Question 8.

Question 9.

Question 10.

Question 1.

Question 2.

Question 3.

Question 4.

Question 5.

Question 6.

Question 7.

Question 8.

Question 9.

Question 10.

Other Topics of that Section

Quick Links

Still have questions about JEE Main ? Ask us.

Related News

Related Articles

Popular Degrees

Popular Specializations

Engineering Colleges in States

Engineering Colleges in Cities

Popular Engineering Exams

Engineering Colleges by College Type