CPCT Full Form

The full form of CPCT is Corresponding Parts of Congruent Triangles. When we study the congruent triangle in Mathematics, we come across the term CPCT. “Corresponding Parts of Congruent Triangles” is known as CPCT. Congruent triangles have equal corresponding parts which is well known.

What is CPCT Full Form?

CPCT Full Form is Corresponding Parts of Congruent Triangles. Most often, the abbreviation CPCT is used in short terms rather than the complete form while discussing triangle topics and answering questions about the same.

A statement or theorem about congruent geometry states that the corresponding sections of congruent triangles are congruent (CPCTC). Therefore, the relationship between the sides and angles of two congruent triangles is referred to as corresponding parts of congruent triangles.

Details about the Congruent Triangles

The most fundamental shapes we learn in mathematics are triangles. Triangles are three-sided closed geometrical figures that can be classified into many forms based on their sides and angles. Equilateral, isosceles, scalene, etc. are examples of common types of triangles. In other words, two triangles are said to be congruent if all three corresponding sides and all three corresponding angles have a similar size. One can move, flip, twist and turn these triangles to produce the same effect.

Congruence is a concept that is used to describe an object and its mirror image. Two things or shapes are known to be congruent if they may be superimposed on one another. Regarding the matter of size and shape, they are the same. In the context of geometric figures, line segments with the same length and angles with the same measure are considered as congruent. This showcases that either object may be systematically aligned with the other object by moving and reflecting it but not by resizing it. So if we can cut out and then perfectly match up two separate plane figures on a piece of paper, they are fit to be called congruent. Also, the paper may be turned over.

A triangle is a polygon with three angles made from three lines. As discussed earlier, when the side lengths and angle measurements of two triangles match, they are said to be congruent. As a consequences, both triangles are prepared for side-by-side and angle-to-angle superimposition. The pictorial representation of the congruent triangles are mentioned below:

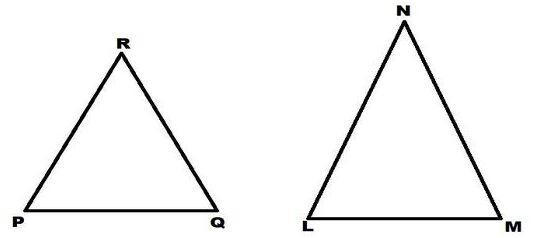
In the above pictures, Δ PQR and Δ LMN are congruent triangles in the aforementioned illustration. This clearly implies that the two triangles PQR and LMN appear to be congruent triangles in the image above, as can be seen. This also demonstrates that the related vertices, P = L, Q = M, and R = N are identical. Additionally, their sides are identical too, 

(PR = LN, PQ = LM, and QR = MN).

Therefore, triangles that have comparable sides and equal angles are said to be congruent. As seen in the example above, PQR ≅ LMN can be written in mathematical connotation. They share a similar space and perimeter.

CPCT Mathematical Rules

Corresponding portions of Congruent triangles are considered as the complete form of CPCT. Triangles can be displayed to be congruent after which the final dimension can be anticipated without actually measuring the triangle's sides and angles.

The following are many congruence rules which are as follows:

• ASA (Angle-Side-Angle)
• AAS (Angle-Angle-Side)
• RHS (Right Angle-Hypotenuse-Side)
• SSS (Side-Side-Side)
• SAS (Side-Angle-Side)

How to know if Two Triangles are not Congruent?

A triangle has only three sides and three angles. If the 4 distinct sides and measures of 4 distinct angles are measured, then it can be inferred that the triangles are not congruent. At some point, these can be measured as it is given in the diagram. On the other side, by the use of the ‘Pythagoras Theorem’ or the triangle internal angle measure, it can find out the measure of missing angles. But in a calculation, sometimes there is not enough information available to know whether the triangles are congruent or not. In the case of drawing out, it becomes complicated to understand and assume that two triangles are not congruent based on the way they appear in the figure. 

Two figures can be said to be congruent only if we can map one onto the other using rigid transformations. As all the rigid transformations preserve distance and a measure of angle, all the corresponding ideas and angles are said to be congruent. The only way to decide the congruency of the triangle is to measure all the sides and angles of the triangle.

Properties of Congruent Triangles

The Congruent Triangles exhibit various properties due to which its properties can be understood in solving Mathematical equations. A few of the properties are listed below:

• ASA (Angle-Side-Angle)

In the Mathematical component, the two triangles are said to be congruent by the ASA (Angle-Side-Angle) rule if any two angles and the side included between the angles of one triangle can be compared to the corresponding two angles and the side included between the angles of the next triangle.

• AAS (Angle-Angle-Side)

Angle-Angle-Side is abbreviated as AAS. The triangles are said to be congruent when two angles and a non-included side of one triangle matches with  the corresponding angles and sides of the second triangle.

• RHS (Right Angle-Hypotenuse-Side)

In simple words, the two right triangles are said to be congruent by the RHS (Right Angle-Hypotenuse Side) rule if the hypotenuse and a side of one right-angled triangle are equal to the hypotenuse and a side of the second right-angled triangle.

• SSS (Side-Side-Side)

According to the SSS rule, two triangles are considered to be congruent if all three sides of one triangle are equal to the corresponding three sides of the another triangle.

• SAS (Side-Angle-Side)

According to the SAS rule, two triangles can be said to be congruent if any two sides and any angle between the sides of one triangle are equal to the corresponding two sides and angle between the sides of another triangle in Mathematics.